さあ、その1を踏まえて・・・ん?プラズマってさあ・・・要は帯電した気体じゃね?って思った…む?これって「それが答えだ!!」ではないか!?
帯電は、物体が電気を帯びる現象である。
別の物体から電子を奪った場合には負に帯電し、逆の場合は正に帯電する。
素粒子の標準模型では、第1世代の荷電レプトンとして位置づけられる。

わかるまで素粒子論「入門編」 第3章 素粒子を分類してみよう
軌道角運動量は粒子の運動によって生じる角運動量だが、スピン角運動量は粒子が本来持っている角運動量なので、位置と運動量で記述する事が出来無い。
スピン角運動量は軌道角運動量と共に、粒子の全角運動量に寄与する。
この「位置と運動量とスピン等の足りないもの」を基本変数とする量子論が「量子力学」である。
基本変数を「場とその時間微分又は共役運動量」に選ぶ量子論、つまり「場の量子論」では電子は粒子では無く「電子場」として記述され、電子場は電磁場の「偏光」(電磁場の向きが右回りに回転するか左回りに回転するか)に似た属性を持つ。
これがスピンであり、場の自転の様なものなので、角運動量を伴う。
その角運動量ベクトルで、スピンの向きと大きさを表す。
このスピンの例で分かる様に、古典的に場であったもの(電磁場等)だけで無く、電子の様な古典的には粒子と見做されて来た物理系であっても、場を基本変数にした方が良く、適用範囲も広い事が判っている。
・・・おいおいおいおいおいおい!!!
何だか良く分からないっつーか、益々マニアックな専門知識が増えて来たぞ!
この状況だと何時になったらプラズマ迄辿り着けるんだ!?
で、又もや専門用語「角運動量」…何かこんなん出る度調べて理解せなならん…うーむ、科学って大変だなあ…
モーメントの定義は「ある点を中心に回転させようとする力の作用」。
これを良く理解する為には、「梃の原理」が用いられます。
物を持ち上げる時支点迄の距離が長い方が、より少ない力を作用せれば良い事に気づくでしょう。
よって、モーメントは「作用させる力×支点までの距離」で求められ、単位は(N・m)等です。
つまり、距離が長ければ長い程作用させるモーメントは大きくなります。
(支点からの腕の長さ)×(力)が両側で等しければ梃は釣り合う。
この「(支点からの腕の長さ)×(力)」がモーメント。
物体を回転させる力と考えれば良いでしょう。
トルクとモーメントは本質的には全く同じものです。
![9911�@���[�����g�Ƃ�.jpg]()
この「(支点からの腕の長さ)×(力)」がモーメント。
物体を回転させる力と考えれば良いでしょう。
トルクとモーメントは本質的には全く同じものです。

原口秀明と原田ミカオの建築×不動産日記9911
トルクは主に工学の分野で使われる用語。
モーメントは物理学で使われる用語です。
但し、トルクは工学分野の言葉なので、単位系も工学に適したものを使うのが一般的です。
力学分野で単に「モーメント」と言った場合には通常はトルクと同じ意味を指します。
モーメントは物理学で使われる用語です。
但し、トルクは工学分野の言葉なので、単位系も工学に適したものを使うのが一般的です。
力学分野で単に「モーメント」と言った場合には通常はトルクと同じ意味を指します。
それ以外のモーメントは「慣性モーメント」や「磁気モーメント」等の様に特に接頭語をつけて区別します。
又トルクと同じ意味のモーメントである事を明示したい場合は特に「力のモーメント」と言う場合があります。
又トルクと同じ意味のモーメントである事を明示したい場合は特に「力のモーメント」と言う場合があります。
又、ある軸まわりのモーメントは、ある軸方向の単位ベクトルを ![\vec{\lambda}]() とすると、混合3重積
とすると、混合3重積![\vec{\lambda} \cdot ( \vec{r} \times \vec{A} )]() で表される。
で表される。
 とすると、混合3重積
とすると、混合3重積 で表される。
で表される。 こちらはスカラー量である。
モーメントは、屡(しばしば)物体の回転運動を記述する際に利用される。
無次元量はスカラー量として扱う。
何じゃいやそりゃっ!!!
・・・無次元数とは、文字通り単位の存在しない数・・・?
流体では、無次元数を考える事は非常に重要になります。
飛行機のまわりや建築物に吹き込む空気の流れを知りたい場合、実物を作って検証するのは大変な為、模型を作って実際に作る前に十分に検証します。
この時、物体の形状が幾何学的に相似である事が重要になります。
この時、物体の形状が幾何学的に相似である事が重要になります。
そして、模型実験での流れが実際に起こる流れと本質的に同じなる様にする事も重要になります。
この様な場合、流れに影響を与える力を絶対数で同じにする事は出来ませんが、最も支配的と考えられる力に関しては、比をとる事で無次元化する事が出来ます。
こうして得られた無次元数を実際の流れと模型の流れとで同じにする事で、実際に起こる流れを推測して、設計に役立たせる事が出来ます・・・う~ん…イマイチ分かり難い…
この様な場合、流れに影響を与える力を絶対数で同じにする事は出来ませんが、最も支配的と考えられる力に関しては、比をとる事で無次元化する事が出来ます。
こうして得られた無次元数を実際の流れと模型の流れとで同じにする事で、実際に起こる流れを推測して、設計に役立たせる事が出来ます・・・う~ん…イマイチ分かり難い…
・・・世界にはその国によって同一のものに対して様々な単位があります。
勿論SI単位で国際的に標準化されてますが、国内では工学単位の様にこれ迄使って来た単位を使う事も少なくない。
長さ:メートル、フィートだと1フィートは=0.3048m 重さ:キログラム、ポンドでは1ポンド=0.45359キログラム
そんな中、同じ二つのものを比較する時に単位系が違っては両者の比較が出来ない為、無次元化によって次元による影響を無くせば、比較が容易になる。
勿論SI単位で国際的に標準化されてますが、国内では工学単位の様にこれ迄使って来た単位を使う事も少なくない。
長さ:メートル、フィートだと1フィートは=0.3048m 重さ:キログラム、ポンドでは1ポンド=0.45359キログラム
そんな中、同じ二つのものを比較する時に単位系が違っては両者の比較が出来ない為、無次元化によって次元による影響を無くせば、比較が容易になる。
…物理学的次元を持った量では、次元の違ったものの間で足し算や引き算が出来ません。
1メートル足す1グラムは意味を成さない足し算ですね。
物理学で実際に計算するには大抵の場合膨大な計算を余儀なくされます。
従って、計算の途中での計算間違いは日常茶飯事にやっています。
そんな時、次元を持ったまま式を表現してしまうと、計算の途中で一々物理的次元を確認しながらやらないと、大混乱に陥ってしまいます。
無次元量で表しておけば、一々次元を確認しなくても何の心配も無く足し算や引き算が出来るのは、大変なメリットです。
物理学では数学を使いますが、数学とは正に数を扱う学問です。
物理学では数学を使いますが、数学とは正に数を扱う学問です。
勿論数には物理的次元が無いので、全て無次元量です。
その数を処理するのに、近年ではコンピューターを使って数値計算をする事が大変重要になっています。
コンピューターは数を処理する機械ですから、そこに代入出来る数値は全て無次元量になっていなくてはなりません。
~私は家の子供達が小さかった頃、良く「象さんは大きいか小さいか」と聞いて遊びました。
初めの内は勿論「象さんは大きい」と答えます。
そうすると私は「でも象さんは学校の校舎より小さいよ、あのビルディングよりも小さいよ」とからかいます。
又「アリンコは小さい」と答えると「でも、黴菌より大きいよ」とからかいます。
そんな事を何度も繰り返している内に、私が似た様な質問をすると、子供達は「何と比べて?」と必ず聞く様になりました。
無次元化された数とは
ある基準になる量と比べて
何倍の値を持つかと言う事を表した数の事です。
ですから、物の大小を言う時には、物理的次元を持った数の値は何も意味が無いのです。
1億分の1gと言う途轍も無く軽い重さでも10億分の1gと比べると重たいからです。
無次元化しておけば、1より小さい数字は基準の量より小さい、1より大きい数字は基準の量より大きいと言う事が出来ます。~
一般に物理学に現れる数学の式は途轍も無く複雑なので、正確に解く事は先ず絶望的です。
そう言う場合でも、式の中で1より十分に小さい量が出て来たら、その量でベキ展開をして、高次のベキに比例した項を無視しても大変良い近似が得られます。
実際の物理学の計算では、殆ど100%この様な近似計算ばかりですから、無次元化した表現を使って、どの項が1より十分に小さいのかを確認する必要があるのです。
極端な言い方をすると、無次元化して置かなくては殆どの場合物理学が語れないと言っても良いくらいです。
極端な言い方をすると、無次元化して置かなくては殆どの場合物理学が語れないと言っても良いくらいです。
・・・ベキ展開?
ベキ??
ベッキーの事?
こう言う「ある大きさ/数等」のX乗にその発生確率が比例する事を「べき乗則」と言う。
人間が関わっている様々な事も乗っている(何と、戦争も!戦死者の数が2倍になるとその頻度は4分の1になるって…マジか!?)以上四コマ漫画及び文章等は勢川びき氏ブログから部分引用
スカラーに話を戻す・・・
特にその相互作用がゲージ理論で記述されている素粒子間において、(仮想粒子として)ゲージ粒子の交換により力が生じる。
奪う事を引き起こす力は別に議論されなければならないが、帯電したまま動かずにいる電気を静電気と言う。
帯電した物体が他の物体を引き寄せる等の性質(クーロン力)を持っている事は、古代から知られていた。
近代になってから、この現象の本格的な研究が始まり、これをきっかけに、電磁気学が発展して行った。
近年ではこうした帯電現象を利用した様々な装置が日常生活に浸透して来ている。
・・・うう~ん…プラズマ迄の道のりは長い…
然しプラズマには電気が絡んでいる事は何となく分かって来たけど、兎に角専門用語が多い!!!
次回で3部作完にしたい。

 の
の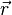 と、点 P における
と、点 P における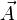 との
との を、O 点まわりの
を、O 点まわりの 